已知椭圆E：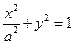
（其中
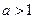），直 线L与椭圆只有一个公共点T；两条平行于y轴的直线
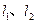分别过椭圆的左、右焦点F1、F2，且直线L分别相交于A、B两点．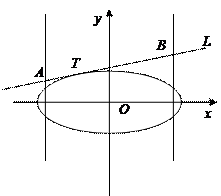
（Ⅰ）若直线L在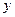
轴上的截距为
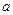，求证：直线L斜率的绝对值与椭圆E的离心率相等；（Ⅱ）若
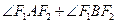的最大值为1200，求椭圆E的方程．
相关试题
的前
项和
的值；
，证明：
中，内角
的对边分别为
，且
的值；
，求向量
方向上的投影．
，
的值．
满足
；
是否为数列
，请写出函数
的值域、最小正周期、单调区间及奇偶性．推荐套卷
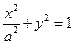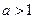已知椭圆E：（其中），直 线L与椭圆只有一个公共点T；两条平行于y轴的直线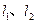分别过椭圆的左、右焦点F1、F2，且直线L分别相交于A、B两点．
（Ⅰ）若直线L在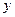轴上的截距为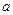，求证：直线L斜率的绝对值与椭圆E的离心率相等；（Ⅱ）若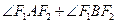的最大值为1200，求椭圆E的方程．
粤公网安备 44130202000953号