（本题12分）如图，在横放得四棱锥E-ABCD中，底面ABCD是正方形，∠DAE=90°,且△ABE是等腰直角三角形，其中∠BAE=90°，连接AC、BD交于点O.
（1）求证：BD⊥平面AEC；
（2）若二面角A-BD-E的大小为60°，且直线EC与平面ABCD所成的角为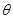
，求
.
，
，且
，
，求角
的值．
是半径为
，圆心角为
的扇形，
是扇形弧上的动点，
是扇形的内接矩形．记
，求当角
取何值时，矩形
．
上，与
轴相切，且被直线
截得的弦长为
的圆的方程．
在一个周期内的图像．
相关知识点
推荐套卷
（本题12分）如图，在横放得四棱锥E-ABCD中，底面ABCD是正方形，∠DAE=90°,且△ABE是等腰直角三角形，其中∠BAE=90°，连接AC、BD交于点O.
（1）求证：BD⊥平面AEC；
（2）若二面角A-BD-E的大小为60°，且直线EC与平面ABCD所成的角为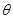，求.
粤公网安备 44130202000953号