如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由
B沿棱柱侧面经过棱C C1到点A1的最短路线长为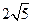 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
点为D.
(1)求三棱柱ABC-A1B1C1的体积;
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.
推荐套卷
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由
B沿棱柱侧面经过棱C C1到点A1的最短路线长为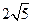 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
点为D.
(1)求三棱柱ABC-A1B1C1的体积;
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.