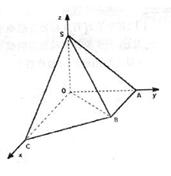
如图直角梯形OABC中，
，SO=1，以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
（Ⅰ）求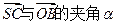
的大小（用反三角函数表示）；
（Ⅱ）设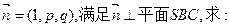
①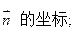
②OA与平面SBC的夹角
（用反三角函数表示）；
③O到平面SBC的距离.
（Ⅲ）设
①
.
②异面直线SC、OB的距离为 .
（注：（Ⅲ）只要求写出答案）.
中,求直线
与平面
所成的角。
直线
，a,b异面，
，
。求证：
。
。求证：
。
的首项
，
， 
是等比数列；
的前
项和
．推荐套卷
如图直角梯形OABC中，，SO=1，以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
（Ⅰ）求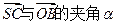的大小（用反三角函数表示）；
（Ⅱ）设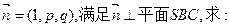
①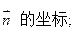
②OA与平面SBC的夹角（用反三角函数表示）；
③O到平面SBC的距离.
（Ⅲ）设
① .
②异面直线SC、OB的距离为 .
（注：（Ⅲ）只要求写出答案）.
粤公网安备 44130202000953号