已知双曲线C的方程为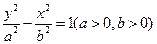
，离心率
，
顶点到渐近线的距离为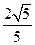
。 求 （1）双曲线C的方程；
(2)如图，P是双曲线C上一点，A，B两点在双曲线C的两条渐近线上，且分别位于第一、二象限，若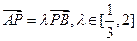
，求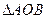
面积的取值范围。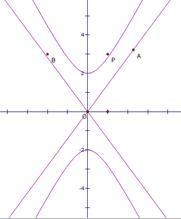
相关试题
（
为实数）.
在
处有极值，求
上是增函数，求
的前
项和为
，点
在直线
．
的通项公式；
图像的相邻两条对称轴之间的距离等于
。
的表达式；（要写出推导过程）
是直角三角形
的内角，求
的值域。
的前项n和为
，若对于任意的正整数n都有
.
，求证：数列
是等比数列，并求出
的前n项和.
，求
相关知识点
推荐套卷
已知双曲线C的方程为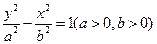，离心率，
顶点到渐近线的距离为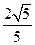。 求 （1）双曲线C的方程；
(2)如图，P是双曲线C上一点，A，B两点在双曲线C的两条渐近线上，且分别位于第一、二象限，若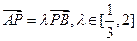，求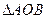面积的取值范围。
粤公网安备 44130202000953号