已知动圆Q经过点A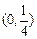
,且与直线
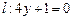相切，动圆圆心Q的轨迹为曲线C，过定点
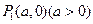作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点
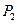,再过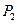作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点
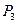,如此继续下去直至无穷，记△
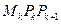的面积为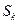
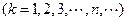
（Ⅰ）求曲线C的方程；
（Ⅱ）试求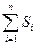
的值。
相关试题
，
时，求函数
的定义域；
，求实数
的取值范围.
是定义在
上的奇函数.
，求实数
的取值范围；
时，
，求
（
）.
时，求函数的最大值和最小值；
的取值范围，使
在区间
上是单调函数.
元，若销售价为
元，可卖出
元，销售量就减少
，用单调性定义证明
在
上是减函数.相关知识点
推荐套卷
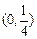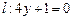已知动圆Q经过点A,且与直线相切，动圆圆心Q的轨迹为曲线C，过定点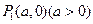作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点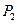,再过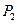作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点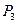,如此继续下去直至无穷，记△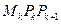的面积为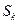
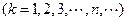
（Ⅰ）求曲线C的方程；
（Ⅱ）试求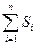的值。
粤公网安备 44130202000953号