直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
（Ⅰ）求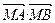
的取值范围；
（Ⅱ）过A、B两点分别作此抛物线的切线，两切线相交于N点.
求证：
；
（Ⅲ）若p是不为1的正整数，当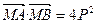
，△ABN的面积的取值范围为［5
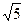，20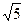］时，求该抛物线的方程.
相关试题
．
的最小正周期；
对任意x∈R，有
，且当
时，
，求
上的解析式．
时，求
的值．
为120°，半径长为6，
的弧长；（2）求弓形OAB的面积．
的图像过点
．
的值；
图像上各点的横坐标变为原来的2倍，纵坐标不变，得到函数
的图像，求函数
上的最大值和最小值．相关知识点
推荐套卷
直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
（Ⅰ）求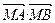的取值范围；
（Ⅱ）过A、B两点分别作此抛物线的切线，两切线相交于N点.
求证：；
（Ⅲ）若p是不为1的正整数，当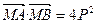，△ABN的面积的取值范围为［5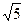，20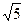］时，求该抛物线的方程.
粤公网安备 44130202000953号