已知抛物线y2=8x上两个动点A、B及一个定点M（x0, y0），F是抛物线的焦点，且|AF|、|MF|、|BF|成等差数列，线段AB的垂直平分线与x轴交于一点N．
（1）求点N的坐标（用x0表示）；
（2）过点N与MN垂直的直线交抛物线于P、Q两点，若|MN|=4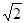
，求△MPQ的面积．
中，已知点
、
、
分别为棱
、
、
的中点.
∥平面
.
，
，求证：平面
⊥平面
的最大值；（2）求
最小值。
的不等式
高
，比较
与
的大小推荐套卷
已知抛物线y2=8x上两个动点A、B及一个定点M（x0, y0），F是抛物线的焦点，且|AF|、|MF|、|BF|成等差数列，线段AB的垂直平分线与x轴交于一点N．
（1）求点N的坐标（用x0表示）；
（2）过点N与MN垂直的直线交抛物线于P、Q两点，若|MN|=4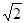，求△MPQ的面积．
粤公网安备 44130202000953号