已知双曲线
的离心率e=2，A，B为双曲线上两点，线段AB的垂直平分线为
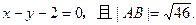
①求双曲线C经过二、四象限的渐近线的倾斜角
②试判断在椭圆C的长轴上是否存在一定点N（a，0），
使椭圆上的动点M满足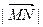
的最小值为3，若存
在求出所有可能的a值，若不存在说明理由.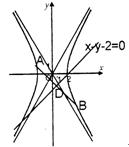
相关试题
是定义在
上的奇函数,当
时，
.
.
中, a，b，c分别是A、B、C的对边，且
.
，
.
；
，求
的取值范围.
的面积为2，且
.
的值.
.
在点
处的切线恒过定点，并求出定点坐标；
在区间
上恒成立，求
的取值范围；
时，求证：在区间
恒成立的函数
推荐套卷
已知双曲线的离心率e=2，A，B为双曲线上两点，线段AB的垂直平分线为
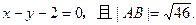
①求双曲线C经过二、四象限的渐近线的倾斜角
②试判断在椭圆C的长轴上是否存在一定点N（a，0），
使椭圆上的动点M满足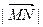的最小值为3，若存
在求出所有可能的a值，若不存在说明理由.
粤公网安备 44130202000953号