给出定义在(0，＋∞)上的三个函数：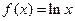
，
，
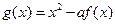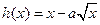，已知
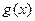在x＝1处取极值.
（Ⅰ）确定函数h(x)的单调性；
（Ⅱ）求证：当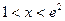
时，恒有
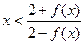成立；
（Ⅲ）把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象，试确定函数y＝g(x)－h1(x)的零点个数，并说明理由.
相关试题
x＋
，h(x)＝
，设F(x)＝f(x)－h(x)，求F(x)的单调区间与极值．推荐套卷
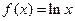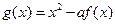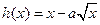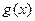给出定义在(0，＋∞)上的三个函数：，，，已知在x＝1处取极值.
（Ⅰ）确定函数h(x)的单调性；
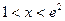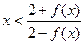（Ⅱ）求证：当时，恒有成立；
（Ⅲ）把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象，试确定函数y＝g(x)－h1(x)的零点个数，并说明理由.
粤公网安备 44130202000953号