某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
相关知识点
推荐套卷
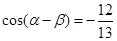 ,
,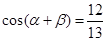 ,且
,且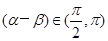 ,
, ,求角
,求角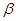 的值.
的值.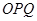 是半径为
是半径为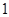 ,圆心角为
,圆心角为 的扇形,
的扇形,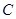 是扇形弧上的动点,
是扇形弧上的动点, 是扇形的内接矩形.记
是扇形的内接矩形.记 ,求当角
,求当角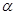 取何值时,矩形
取何值时,矩形
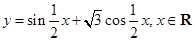 .
.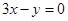 上,与
上,与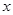 轴相切,且被直线
轴相切,且被直线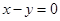 截得的弦长为
截得的弦长为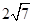 的圆的方程.
的圆的方程. 在一个周期内的图像.
在一个周期内的图像.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号