已知函数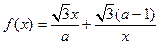 (
(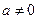 且
且 ).
).
(1) 试就实数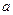 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当 时,函数在
时,函数在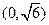 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求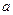 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线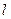 ,使得
,使得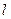 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出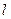 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
推荐套卷
已知函数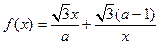 (
(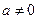 且
且 ).
).
(1) 试就实数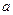 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当 时,函数在
时,函数在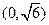 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求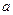 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线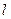 ,使得
,使得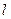 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出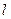 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.