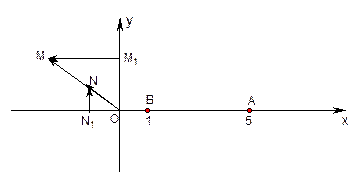在直角坐标平面上，O为原点，M为动点，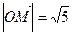
，
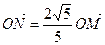．过点M作MM1⊥
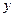轴于M1，过N作NN1⊥
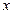轴于点N1，
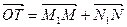．记点T的轨迹为曲线C，点A（5，0）、B（1，0），过点A作直线
交曲线C于两个不同的点P、Q（点Q在A与P之间）．
（Ⅰ）求曲线C的方程；
（Ⅱ）证明不存在直线，使得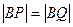
；
（Ⅲ）过点P作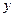轴的平行线与曲线C的另一交点为S，若
，证明
．
相关试题
，命题
：对任意
，不等式
恒成立；命题
：存在
，使不等式
成立．
的取值范围；
为假，
为真，求
的相邻两项
、
是关于
的方程
的两根，且
。
是等比数列；
项的
和及数列
的通项公式。
，记
。
，求
的值；
中，角
、
、
的对边分别为
、
、
，且满足
，
，
，试求
.（
为常数,
）
是函数
的一个极值点，求
时，
上是增函数；
，总存在
，使不等式
成立，求实数
的取值范围.
的前
项和为
，且满足
，
，数列
的前
，若
对一切
恒成立，求
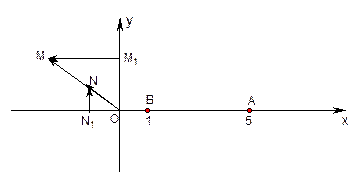
的最小值．推荐套卷
在直角坐标平面上，O为原点，M为动点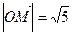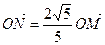，，．过点M作MM1⊥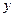轴于M1，过N作NN1⊥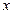轴于点N1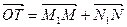，．记点T的轨迹为曲线C，点A（5，0）、B（1，0），过点A作直线交曲线C于两个不同的点P、Q（点Q在A与P之间）．
（Ⅰ）求曲线C的方程；
（Ⅱ）证明不存在直线，使得；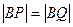
（Ⅲ）过点P作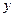轴的平行线与曲线C的另一交点为S，若，证明．
粤公网安备 44130202000953号