已知A(x1,f(x1))，B(x2,f(x2))是函数f(x)=2sin(wx+j)(w＞0,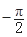
＜j＜0)图象上的任意两点，且角j的终边经过点P(l，-
)，若|f(x1)-f(x2)|=4时，|x1-x2|的最小值为
.
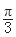(1)求函数f(x)的解析式；(2)求函数f(x)的单调递增区间；(3)当x∈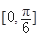
时，不等式mf(x)+2m≥f(x)恒成立，求实数m的取值范围.
在定义域内且x∈[0,2π]的图象．
的图象．
，求实数a的取值范围．
cos3x＋
；
＋1.
) 的奇偶性．相关知识点
推荐套卷
已知A(x1,f(x1))，B(x2,f(x2))是函数f(x)=2sin(wx+j)(w＞0,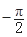＜j＜0)图象上的任意两点，且角j的终边经过点P(l，-)，若|f(x1)-f(x2)|=4时，|x1-x2|的最小值为.
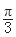(1)求函数f(x)的解析式；(2)求函数f(x)的单调递增区间；(3)当x∈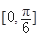时，不等式mf(x)+2m≥f(x)恒成立，求实数m的取值范围.
粤公网安备 44130202000953号