（本小题满分12分）
在数列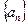
中，已知a1=2，an+1=4an－3n＋1，n∈
.
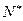（1）设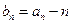
，求数列
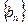的通项公式;
（2）设数列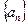的前n项和为Sn，证明：对任意的n∈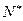，不等式Sn+1≤4Sn恒成立．
，2tanα＋3sinβ＝7，且tanα－6sinβ＝1，求sinα的值．
－
.
>0；
.
； (2)y＝lg(3－4sin2x)．相关知识点
推荐套卷
（本小题满分12分）
在数列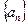中，已知a1=2，an+1=4an－3n＋1，n∈.
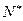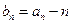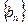（1）设，求数列的通项公式;
（2）设数列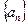的前n项和为Sn，证明：对任意的n∈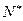，不等式Sn+1≤4Sn恒成立．
粤公网安备 44130202000953号