已知双曲线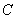 的方程为
的方程为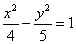 ,若直线
,若直线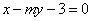 截双曲线的一支所得弦长为5
截双曲线的一支所得弦长为5
(I)求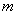 的值;
的值;
(II)设过双曲线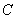 上的一点
上的一点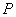 的直线与双曲线的两条渐近线分别交于
的直线与双曲线的两条渐近线分别交于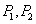 ,且点
,且点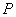 分有向线段
分有向线段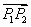 所成的比为
所成的比为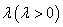 。当
。当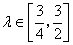 时,求
时,求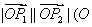 为坐标原点)的最大值和最小值
为坐标原点)的最大值和最小值
相关知识点
推荐套卷
已知双曲线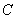 的方程为
的方程为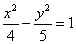 ,若直线
,若直线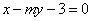 截双曲线的一支所得弦长为5
截双曲线的一支所得弦长为5
(I)求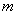 的值;
的值;
(II)设过双曲线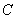 上的一点
上的一点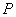 的直线与双曲线的两条渐近线分别交于
的直线与双曲线的两条渐近线分别交于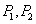 ,且点
,且点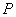 分有向线段
分有向线段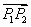 所成的比为
所成的比为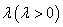 。当
。当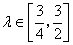 时,求
时,求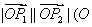 为坐标原点)的最大值和最小值
为坐标原点)的最大值和最小值