某校设计了一个实验学科的实验考查方案：考生从
道备选题中一次性随机抽取
题，按照题目要求独立完成全部实验操作. 规定：至少正确完成其中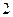
题的便可通过考查. 已知道备选题中考生甲有
题能正确完成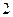，题不能完成；考生乙每题正确完成的概率都是
，且每题正确完成与否互不影响. 求：
（1）分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望；
（2）试用统计知识分析比较两考生的实验操作能力.
相关试题
中，
是等比数列，并求数列
满足
，数列
项和为
，若不等式
对一切
恒成立，求
的取值范围．
中，侧棱
平面
，
为等腰直角三角形，
，且
分别是
的中点．
平面
；
的余弦值．
的前n项和为
，且
．
，数列
的前
项和为
，证明：
的不等式
所在平面外一点
，
平面
分别是
的中点，
．
平面
，求直线
与平面
所成角的正弦值．推荐套卷
某校设计了一个实验学科的实验考查方案：考生从道备选题中一次性随机抽取题，按照题目要求独立完成全部实验操作. 规定：至少正确完成其中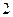题的便可通过考查. 已知道备选题中考生甲有题能正确完成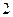，题不能完成；考生乙每题正确完成的概率都是，且每题正确完成与否互不影响. 求：
（1）分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望；
（2）试用统计知识分析比较两考生的实验操作能力.
粤公网安备 44130202000953号