某食品厂每天需用食品配料200千克，配料的价格为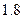
元/千克，每次进货需支付运费236元.每次购买来的配料还需支付保管费用，其标准如下: 7天以内（含7天），无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.(Ⅰ）当9天购买一次配料时，求该厂用于配料的保管费用P是多少元？
(Ⅱ）设该厂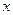
天购买一次配料，求该厂在这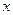天中用于配料的总费用
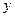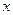（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
值集合； （5）求函数的单调区间；
，求
的取值范围
的图象作怎样的变换可以得到函数
的图象？
的定义域、周期和单调区间
，求
的值推荐套卷
某食品厂每天需用食品配料200千克，配料的价格为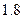元/千克，每次进货需支付运费236元.每次购买来的配料还需支付保管费用，其标准如下: 7天以内（含7天），无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.(Ⅰ）当9天购买一次配料时，求该厂用于配料的保管费用P是多少元？
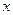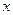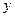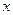(Ⅱ）设该厂天购买一次配料，求该厂在这天中用于配料的总费用（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
粤公网安备 44130202000953号