某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台,现销售给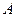 地10台,
地10台,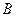 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至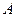 地,
地,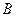 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至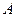 地,
地,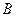 地的费用分别为300元和500元.
地的费用分别为300元和500元.
(1) 设从乙地调运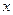 台至
台至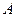 地,求总费用
地,求总费用 关于台数
关于台数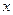 的函数解析式;
的函数解析式;
(2) 若总运费不超过9000元,问共有几种调运方案;
(3) 求出总运费最低的调运方案及最低的费用.
相关知识点
推荐套卷
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台,现销售给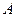 地10台,
地10台,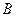 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至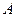 地,
地,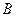 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至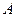 地,
地,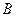 地的费用分别为300元和500元.
地的费用分别为300元和500元.
(1) 设从乙地调运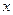 台至
台至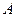 地,求总费用
地,求总费用 关于台数
关于台数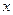 的函数解析式;
的函数解析式;
(2) 若总运费不超过9000元,问共有几种调运方案;
(3) 求出总运费最低的调运方案及最低的费用.