如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系 .点
.点 在正方体的对角线
在正方体的对角线 上,点
上,点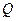 在正方体的棱
在正方体的棱 上.
上.
(1) 当点 为对角线
为对角线 的中点,点
的中点,点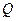 在棱
在棱 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(2) 当点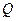 为棱
为棱 的中点,点
的中点,点 在对角线
在对角线 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(3) 当点 在对角线
在对角线 上运动,点
上运动,点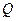 在棱
在棱 上运动时,探究
上运动时,探究 的最小值.
的最小值.
由以上问题,你得到了什么结论?你能证明你的结论吗?
相关知识点
推荐套卷
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系 .点
.点 在正方体的对角线
在正方体的对角线 上,点
上,点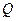 在正方体的棱
在正方体的棱 上.
上.
(1) 当点 为对角线
为对角线 的中点,点
的中点,点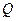 在棱
在棱 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(2) 当点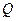 为棱
为棱 的中点,点
的中点,点 在对角线
在对角线 上运动时,探究
上运动时,探究 的最小值;
的最小值;
(3) 当点 在对角线
在对角线 上运动,点
上运动,点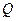 在棱
在棱 上运动时,探究
上运动时,探究 的最小值.
的最小值.
由以上问题,你得到了什么结论?你能证明你的结论吗?