（本小题满分13分）对于在区间[m，n]上有意义的两个函数
与
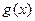，如果对任意
[m，n]均有
，称与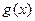在[m，n]上是接近的，否则称与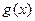在[m，n]上是非接近的，现有两个函数
与
（a＞0，a≠1），给定区间[a＋2，a＋3]．（1）若
与
在给定区间[a＋2，a＋3]上都有意义，求a的取值范围；（2）讨论与在[a＋2，a＋3]上是否是接近的．
相关试题
，求圆C的半径．
，向量
是矩阵
的属性特征值
的一个特征向量，矩阵
以及它的另一个特征值．
中，
，
交
于点D
∽
均为正数，且
，证明：
，则
；
的充要条件．推荐套卷
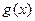（本小题满分13分）对于在区间[m，n]上有意义的两个函数与，如果对任意[m，n]均有，称与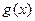在[m，n]上是接近的，否则称与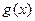在[m，n]上是非接近的，现有两个函数与（a＞0，a≠1），给定区间[a＋2，a＋3]．（1）若与在给定区间[a＋2，a＋3]上都有意义，求a的取值范围；（2）讨论与在[a＋2，a＋3]上是否是接近的．
粤公网安备 44130202000953号