已知平面
上的动点
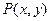及两定点A（-2，0），B（2，0），直线PA，PB的斜率分别是
，
，且·
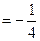。（1）求动点P的轨迹C的方程；
（2）已知直线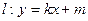
与曲线C交于M，N两点，且直线BM，BN的斜率都存在并满足
·
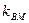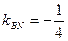，求证：直线
过原点。
相关试题
边上的高所在直线方程；
边上的中线所在直线方程；
，
分别为边
和
的方程
是空集，求
的取值范围；
，
，
，
的取值范围
在极坐标系中的方程为
，圆C在极坐标系中的方程为
，求圆C被直线
和直线l垂直的直线方程；推荐套卷
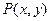已知平面上的动点及两定点A（-2，0），B（2，0），直线PA，PB的斜率分别是，，且·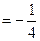。（1）求动点P的轨迹C的方程；
（2）已知直线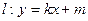与曲线C交于M，N两点，且直线BM，BN的斜率都存在并满足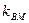·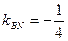，求证：直线过原点。
粤公网安备 44130202000953号