多项飞碟是奥运会的竞赛项目,它是由抛靶机把碟靶(射击的目标)在一定范围内从不同的方向飞出,每抛出一个碟靶,就允许运动员射击两次.一运动员在进行训练时,每一次射击命中碟靶的概率P与运动员离碟靶的距离S(米)成反比,现有一碟靶抛出后S(米)与飞行时间t(秒)满足S=15(t+1),(0≤t≤4).假设运动员在碟靶飞出后0.5秒进行第一次射击,且命中的概率为0.8,如果他发现没有命中,则通过迅速调整,在第一次射击后经过0.5秒进行第二次射击,求他命中此碟靶的概率?
相关知识点
推荐套卷
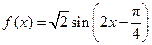 在一个周期内的图像.
在一个周期内的图像.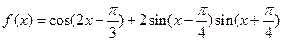
 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程 上的值域
上的值域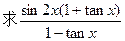 的值.
的值.
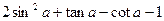 的值.
的值.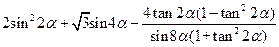 .=
.=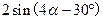
 粤公网安备 44130202000953号
粤公网安备 44130202000953号