已知大西北某荒漠上 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以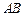 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
(1)试求四边形另两个顶点的轨迹方程;
(2)该荒漠上有一条直线型小溪 刚好通过点
刚好通过点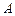 ,且
,且 与
与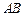 成
成 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
推荐套卷
已知大西北某荒漠上 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以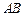 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
(1)试求四边形另两个顶点的轨迹方程;
(2)该荒漠上有一条直线型小溪 刚好通过点
刚好通过点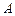 ,且
,且 与
与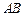 成
成 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?