某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件件次品则损失100元,已知该厂制造电子元件过程中,次品率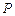 与日产量
与日产量 的函数关系是
的函数关系是 .
.
(1)将该厂的日盈利额T(元)表示为日产量 (件)的函数;
(件)的函数;
(2)为获最大盈利,该厂的日产量应定为多少件?
推荐套卷
某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件件次品则损失100元,已知该厂制造电子元件过程中,次品率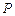 与日产量
与日产量 的函数关系是
的函数关系是 .
.
(1)将该厂的日盈利额T(元)表示为日产量 (件)的函数;
(件)的函数;
(2)为获最大盈利,该厂的日产量应定为多少件?