等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S.
（1）求函数S=f(x)的解析式；
（2）试确定点P的位置，使△ABP的面积S最大.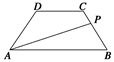
满足条件
，
，
，设
的通项公式；
。
且
≠1)
的单调性。
的图象过原点。
的值；
，
，
成等差数列，求
的值。
的定义域为
。
的值域；
，命题
， 若 
是 
的必要不充分条件，求实数
的取值范围。推荐套卷
等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S.
（1）求函数S=f(x)的解析式；
（2）试确定点P的位置，使△ABP的面积S最大.
粤公网安备 44130202000953号