某工厂生产一种机器的固定成本（即固定投入）为0.5万元，但每生产100台，需要加可变成本（即另增加投入）0.25万元.市场对此产品的年需求量为500台，销售的收入函数为R（x）=5x-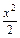
（万元）(0≤x≤5)，其中x是产品售出的数量（单位：百台）.
（1）把利润表示为年产量的函数；
（2）年产量是多少时，工厂所得利润最大？
（3）年产量是多少时，工厂才不亏本？
相关试题
的图象；
，
，
.
，
；
，求
的取值范围.
的定义域．
，过点
且不与坐标轴垂直的直线
交椭圆
于
两点，设点
关于
轴的对称点为
，
过
面积的取值范围。
推荐套卷
某工厂生产一种机器的固定成本（即固定投入）为0.5万元，但每生产100台，需要加可变成本（即另增加投入）0.25万元.市场对此产品的年需求量为500台，销售的收入函数为R（x）=5x-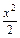（万元）(0≤x≤5)，其中x是产品售出的数量（单位：百台）.
（1）把利润表示为年产量的函数；
（2）年产量是多少时，工厂所得利润最大？
（3）年产量是多少时，工厂才不亏本？
粤公网安备 44130202000953号