如图所示,设抛物线方程为x2="2py" (p＞0),M为直线y=-2p上任意一点,过M
引抛物线的切线,切点分别为A,B.
(1)求证:A,M,B三点的横坐标成等差数列；
(2)已知当M点的坐标为(2,-2p)时,|AB|=4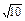
.求此时抛物线的方程.
相关知识点
推荐套卷
如图所示,设抛物线方程为x2="2py" (p＞0),M为直线y=-2p上任意一点,过M
引抛物线的切线,切点分别为A,B.
(1)求证:A,M,B三点的横坐标成等差数列；
(2)已知当M点的坐标为(2,-2p)时,|AB|=4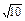.求此时抛物线的方程.
粤公网安备 44130202000953号