如图所示，已知四棱锥
，底面
为菱形，
平面
，
,
分别是
的中点.
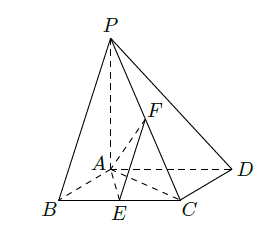
(1)证明:
;
(2)若
为
上的动点,
与平面
所成最大角的正切值为
,
求二面角
的余弦值.
相关试题
圆心在直线
上，且过点
，
. 
与圆
、
两点，
为坐标原点，且
，求
的值．
中，角
的对边分别为
,且
．
，求
；
，求
的值.
的图象经过点
和
，记
的通项公式；
，若
，求
的最小值；
对一切
均成立的最大实数
.
满足递推式
，其中
；
并求数列
有
求数列
的前n项和
.
满足
，且关于
的方程
的两实数根分别在区间（-3，-2），（0，1）内。
的取值范围；
在区间（-1-
，1-推荐套卷
如图所示，已知四棱锥
，底面
为菱形，
平面
，
,
分别是
的中点.
(1)证明:
;
(2)若
为
上的动点,
与平面
所成最大角的正切值为
,
求二面角
的余弦值.
粤公网安备 44130202000953号