如图所示,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所 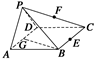 在平面垂直于底面ABCD,若G为AD边的中点,
在平面垂直于底面ABCD,若G为AD边的中点,
(1)求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
相关知识点
推荐套卷
如图所示,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所  在平面垂直于底面ABCD,若G为AD边的中点,
在平面垂直于底面ABCD,若G为AD边的中点,
(1)求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.