某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数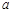 的值.(参考数据:ln2»0.69,ln10»2.3)
的值.(参考数据:ln2»0.69,ln10»2.3)