位同学参加某种形式的竞赛，竞赛规则规定：每位同学必须从甲、乙两道
题中任选一题作答，选甲题答对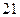得
分，答错得
分；选乙题答对得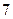
分，答错得
分．若位同学的总分为
，求这位同学不
同得分情况的种数。
相关试题
上的函数
，对于任意的实数
，恒有
，且当
时，
。
及
的值域。
，
，
,求
的范围。
的不等式
（其中
是常数，且
）
上的函数
满足
，且当
时，
，
上的表达式;
，且
,求实数
的取值范围。
，求使
成立的
的取值范围。
是
上的增函数，设
。
用定义证明：
证明：如果
，则
>0，相关知识点
推荐套卷
位同学参加某种形式的竞赛，竞赛规则规定：每位同学必须从甲、乙两道题中任选一题作答，选甲题答对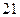得分，答错得分；选乙题答对得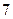分，答错得分．若位同学的总分为，求这位同学不同得分情况的种数。
粤公网安备 44130202000953号