在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率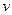 (单位:cm
(单位:cm /s)与管道半径
/s)与管道半径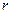 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比.
(1) 写出气流速度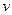 关于管道半径
关于管道半径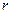 的函数解析式;
的函数解析式;
(2) 若气体在半径为3cm的管道中,流量速率为400cm /s,求该气体通过半
/s,求该气体通过半
径为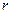 的管道时,其流量速率
的管道时,其流量速率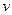 的表达式;
的表达式;
(3) 已知(2)中的气体通过的管道半径为5cm,计算该气体的流量速率.
推荐套卷
在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率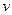 (单位:cm
(单位:cm /s)与管道半径
/s)与管道半径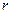 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比.
(1) 写出气流速度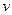 关于管道半径
关于管道半径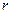 的函数解析式;
的函数解析式;
(2) 若气体在半径为3cm的管道中,流量速率为400cm /s,求该气体通过半
/s,求该气体通过半
径为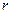 的管道时,其流量速率
的管道时,其流量速率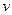 的表达式;
的表达式;
(3) 已知(2)中的气体通过的管道半径为5cm,计算该气体的流量速率.