为了保护环境,某校环保小组成员小沅收集废电池,第一天收集 号电池
号电池 节,
节, 号电池
号电池 节,总质量为
节,总质量为 ;第二天收集
;第二天收集 号电池
号电池 节,
节, 号电池
号电池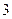 节,总质量为
节,总质量为 .
.
(1) 求 号电池和
号电池和 号电池每节质量各为多少克?
号电池每节质量各为多少克?
(2) 学校环保小组为估计四月份收集电池的总质量,随机抽取了该月某 天收
天收
集废电池的节数如下表:
 号废电池(单位:节) 号废电池(单位:节) |
 |
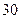 |
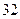 |
 |
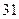 |
 号废电池(单位:节) 号废电池(单位:节) |
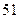 |
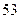 |
 |
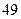 |
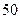 |
分别计算这 天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?
天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?
推荐套卷
 .
. 的奇偶性;
的奇偶性; ), 求
), 求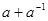 的值.
的值.
 在
在 上是增函数;
上是增函数; 上取得最大值为5,求实数
上取得最大值为5,求实数 的值.
的值.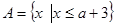 ,
,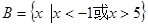 .
.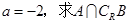 ; (2) 若
; (2) 若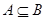 ,求
,求 的取值范围.
的取值范围. ;
; 
 粤公网安备 44130202000953号
粤公网安备 44130202000953号