过椭圆 的左焦点
的左焦点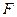 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦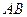 ,若点
,若点 在
在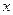 轴上,且使得
轴上,且使得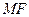 为
为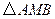 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”.
为该椭圆的“左特征点”.
(1)求椭圆 的“左特征点”
的“左特征点” 的坐标;
的坐标;
(2)试根据(1)中的结论猜测:椭圆 的“左特征点”
的“左特征点” 是一个怎样的点?
是一个怎样的点?
并证明你的结论.
推荐套卷
过椭圆 的左焦点
的左焦点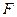 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦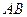 ,若点
,若点 在
在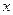 轴上,且使得
轴上,且使得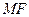 为
为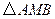 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”.
为该椭圆的“左特征点”.
(1)求椭圆 的“左特征点”
的“左特征点” 的坐标;
的坐标;
(2)试根据(1)中的结论猜测:椭圆 的“左特征点”
的“左特征点” 是一个怎样的点?
是一个怎样的点?
并证明你的结论.