凸
边形
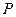中的每条边和每条对角线都被染为n种颜色中的一种颜色．问：对怎样的n，存在一种染色方式，使得对于这n种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形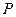的顶点，且它的3条边分别被染为这3种颜色？
相关试题
取何值，曲线
总通过定点．
的距离减去它到
轴的距离的差是
，求这曲线的方程．
，
分别过点
，
（
为常数），且分别绕
，
旋转，它们分别交
轴于
，
（
，
为参数），若
，求两直线交点
的轨迹方程．
的半径为
的定圆
的两互相垂直的直径，作动弦
交
于
，引
，且交
于
，求点
（元）与行李重量
的关系用直线
的方程表示，试求：
（1）直线相关知识点
推荐套卷
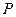凸边形中的每条边和每条对角线都被染为n种颜色中的一种颜色．问：对怎样的n，存在一种染色方式，使得对于这n种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形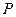的顶点，且它的3条边分别被染为这3种颜色？
粤公网安备 44130202000953号