对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数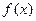 称为
称为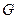 函数。
函数。
① 对任意的 ,总有
,总有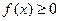 ;
;
② 当 时,总有
时,总有 成立。
成立。
已知函数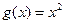 与
与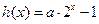 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数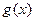 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数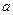 组成的集合;
组成的集合;
(3)在(2)的条件下,讨论方程
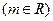 解的个数情况。
解的个数情况。
相关知识点
推荐套卷
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数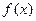 称为
称为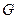 函数。
函数。
① 对任意的 ,总有
,总有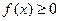 ;
;
② 当 时,总有
时,总有 成立。
成立。
已知函数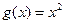 与
与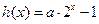 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数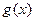 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数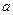 组成的集合;
组成的集合;
(3)在(2)的条件下,讨论方程
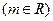 解的个数情况。
解的个数情况。