(本小题满分14分) 已知函数 及正整数数列
及正整数数列 . 若
. 若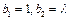 ,且当
,且当 时,有
时,有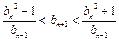 ; 又
; 又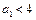 ,
, ,且
,且 对任意
对任意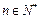 恒成立. 数列
恒成立. 数列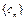 满足:
满足: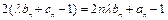 .
.
(1) 求数列 及
及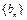 的通项公式;
的通项公式;
(2) 求数列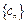 的前
的前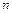 项和
项和 ;
;
(3) 证明存在 ,使得
,使得 对任意
对任意 均成立.
均成立.
推荐套卷
(本小题满分14分) 已知函数 及正整数数列
及正整数数列 . 若
. 若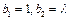 ,且当
,且当 时,有
时,有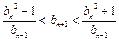 ; 又
; 又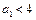 ,
, ,且
,且 对任意
对任意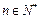 恒成立. 数列
恒成立. 数列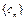 满足:
满足: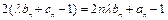 .
.
(1) 求数列 及
及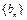 的通项公式;
的通项公式;
(2) 求数列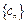 的前
的前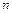 项和
项和 ;
;
(3) 证明存在 ,使得
,使得 对任意
对任意 均成立.
均成立.