某商场预计2013年1月份起前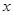
个月，顾客对某种商品的需求总量
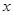（单位：件）与的关系近似地满足：
.该商品第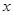月的进货单价
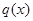（单位：元）与x的近似关系是：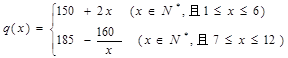
（1）写出今年第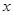月的需求量
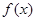件与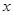的函数关系式；
（2）该商品每件的售价为185元，若不计其他费用且每月都能满足市场需求，试问商场2013年第几月份销售该商品的月利润最大，最大月利润为多少元？
相关试题
中，
、
为棱
、
的中点．
∥平面
；
⊥平面
，且和圆C：
相交，截得弦长为
，求l的方程.
f(2x)
在
上为减函数。
上的最小值.
：
与直线
：
的交点
，且满足下列条件的直线方程
平行 ； 
经过点
，其左、右顶点分别是
、
，左、右焦点分别是
、
，
（异于
交直线
于
、
两点,若
成等比数列.
为直径的圆过点推荐套卷
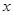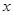某商场预计2013年1月份起前个月，顾客对某种商品的需求总量（单位：件）与的关系近似地满足：.该商品第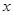月的进货单价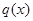（单位：元）与x的近似关系是：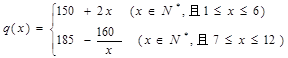
（1）写出今年第月的需求量件与的函数关系式；
（2）该商品每件的售价为185元，若不计其他费用且每月都能满足市场需求，试问商场2013年第几月份销售该商品的月利润最大，最大月利润为多少元？
粤公网安备 44130202000953号