给定锐角三角形PBC，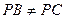
．设A，D分别是边PB，PC上的点，连接AC，BD，相交于点O. 过点O分别作OE⊥AB，OF⊥CD，垂足分别为E，F，线段BC，AD的中点分别为M，N．
（1）若A，B，C，D四点共圆，求证：
；
（2）若，是否一定有A，B，C，D四点共圆？证明你的结论．
相关试题
(φ为参数)的右焦点，且与直线
(t为参数)平行的直线的普通方程．
，半径R＝
，求圆C的极坐标方程．
≤a恒成立，求a的取值范围．推荐套卷
给定锐角三角形PBC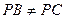，．设A，D分别是边PB，PC上的点，连接AC，BD，相交于点O. 过点O分别作OE⊥AB，OF⊥CD，垂足分别为E，F，线段BC，AD的中点分别为M，N．
（1）若A，B，C，D四点共圆，求证：；
（2）若，是否一定有A，B，C，D四点共圆？证明你的结论．
粤公网安备 44130202000953号