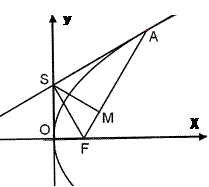
如图, 是抛物线
是抛物线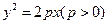 的焦点,过
的焦点,过 轴上的动点
轴上的动点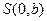 作直线
作直线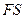 的垂线
的垂线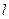 .
.
(Ⅰ)求证:直线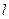 与抛物线
与抛物线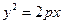 相切;
相切;
(Ⅱ)设直线 与抛物线
与抛物线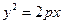 相切于点
相切于点 ,过点
,过点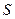 作直线
作直线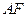 的垂线,垂足为
的垂线,垂足为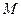 ,求线段
,求线段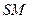 的长度以及动点
的长度以及动点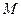 的轨迹方程.
的轨迹方程.
相关知识点
推荐套卷
如图,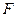 是抛物线
是抛物线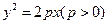 的焦点,过
的焦点,过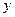 轴上的动点
轴上的动点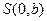 作直线
作直线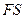 的垂线
的垂线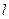 .
.
(Ⅰ)求证:直线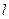 与抛物线
与抛物线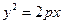 相切;
相切;
(Ⅱ)设直线 与抛物线
与抛物线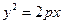 相切于点
相切于点 ,过点
,过点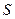 作直线
作直线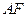 的垂线,垂足为
的垂线,垂足为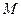 ,求线段
,求线段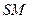 的长度以及动点
的长度以及动点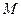 的轨迹方程.
的轨迹方程.