(12分)已知AB是椭圆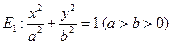 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为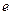 ,求
,求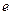 关于
关于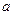 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
推荐套卷
(12分)已知AB是椭圆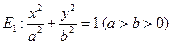 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为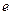 ,求
,求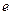 关于
关于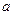 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.