若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数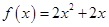 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列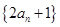 是“平方递推数列”,且数列
是“平方递推数列”,且数列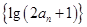 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项之积为
项之积为 ,即
,即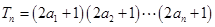 ,求数列
,求数列 的通项及
的通项及 关于
关于 的表达式;
的表达式;
(3)记 ,求数列
,求数列 的前
的前 项和
项和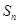 ,并求使
,并求使 的
的 的最小值.
的最小值.
推荐套卷
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数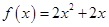 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列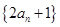 是“平方递推数列”,且数列
是“平方递推数列”,且数列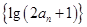 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项之积为
项之积为 ,即
,即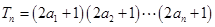 ,求数列
,求数列 的通项及
的通项及 关于
关于 的表达式;
的表达式;
(3)记 ,求数列
,求数列 的前
的前 项和
项和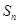 ,并求使
,并求使 的
的 的最小值.
的最小值.