如图，三条直线a、b、c两两平行，直线a、b间的距离为p，直线b、c间的距离为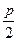
，A、B为直线a上两定点，且｜AB｜=2p，MN是在直线b上滑动的长度为2p的线段。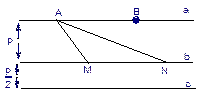 
（1）建立适当的平面直角坐标系，求△AMN的外心C的轨迹E；
（2）接上问，当△AMN的外心C在E上什么位置时，d+｜BC｜最小，最小值是多少？（其中d是外心C到直线c的距离）.
相关试题
．
的单调递减区间；
，都有
成立，求实数
的取值范围．
（
）的部分图像如图所示．
的解析式； 
，且
，求
的值．
cos xsin x－
cos 2x
的最小正周期；
上的最大值、最小值及此时相应自变量x的取值
都是第一象限的角，求
相关知识点
推荐套卷
如图，三条直线a、b、c两两平行，直线a、b间的距离为p，直线b、c间的距离为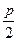，A、B为直线a上两定点，且｜AB｜=2p，MN是在直线b上滑动的长度为2p的线段。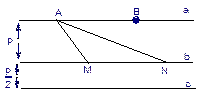
（1）建立适当的平面直角坐标系，求△AMN的外心C的轨迹E；
（2）接上问，当△AMN的外心C在E上什么位置时，d+｜BC｜最小，最小值是多少？（其中d是外心C到直线c的距离）.
粤公网安备 44130202000953号