设椭圆C1的方程为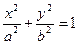 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=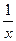 ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式.
推荐套卷
设椭圆C1的方程为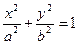 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=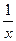 ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式.