袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是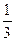 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(i)求恰好摸5次停止的概率;
(ii)记5次之内(含5次)摸到红球的次数为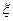 ,求随机变量
,求随机变量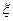 的分布率及数学期望E
的分布率及数学期望E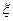 .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是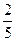 ,求p的值.
,求p的值.
相关知识点
推荐套卷
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是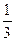 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(i)求恰好摸5次停止的概率;
(ii)记5次之内(含5次)摸到红球的次数为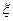 ,求随机变量
,求随机变量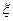 的分布率及数学期望E
的分布率及数学期望E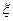 .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是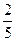 ,求p的值.
,求p的值.