已知双曲线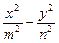
=1(m＞0,n＞0)的顶点为A1、A2，与y轴平行的直线l交双曲线于点P、Q.
(1)求直线A1P与A2Q交点M的轨迹方程；
(2)当m≠n时，求所得圆锥曲线的焦点坐标、准线方程和离心率.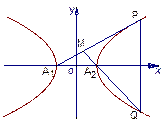
相关试题
，其中
，
，并且线段
所在直线的斜率为
．
的通项公式
的前
项和为
，求
的不等式
的解集是一个开区间
，定义开区间
的长度
。
（
表示），并写出其定义域；
，求实数
中，
沿
折起，使平面
⊥平面
.
⊥平面
的大小；
是侧棱
中点，求直线
与平面
所成角的正弦值.
圆心在直线
上，且过点
，
. 
与圆
、
两点，
为坐标原点，且
，求
的值．
中，角
的对边分别为
,且
．
，求
；
，求
的值.相关知识点
推荐套卷
已知双曲线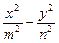=1(m＞0,n＞0)的顶点为A1、A2，与y轴平行的直线l交双曲线于点P、Q.
(1)求直线A1P与A2Q交点M的轨迹方程；
(2)当m≠n时，求所得圆锥曲线的焦点坐标、准线方程和离心率.
粤公网安备 44130202000953号