如图所示是某班学生一次数学考试成绩的频率分布直方图，
其中纵轴表示学生数，观察图形，回答下列问题：
（1）全班有多少学生； （2）此次考试平均成绩大概是多少；
（3）不及格的人数有多少？占全班多大比例？
（4）如果80分以上的成绩为优良， 那么这个班的优良率为多少？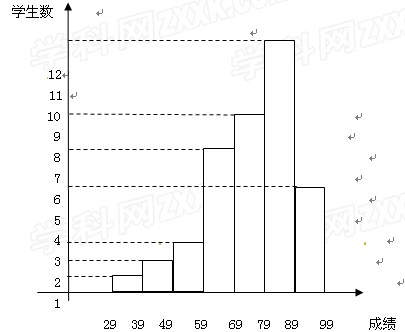
，
，求：角A、B、C的大小。
的最小正周期
．
的值；
是
的最小内角，求函数
的值域．
，复数
，且
在复平面上所对应点在直线
上，求
的取值范围。
是平面上的两个向量，且
互为垂直.
的值；（2）若
的值.
.
，求函数
的值；（2）求函数
的自变量
的值.推荐套卷
如图所示是某班学生一次数学考试成绩的频率分布直方图，
其中纵轴表示学生数，观察图形，回答下列问题：
（1）全班有多少学生； （2）此次考试平均成绩大概是多少；
（3）不及格的人数有多少？占全班多大比例？
（4）如果80分以上的成绩为优良， 那么这个班的优良率为多少？
粤公网安备 44130202000953号