设数列{an}的前n项和Sn=na+n(n－1)b，(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,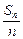
－1)为坐标的点Pn(n=1,2,…)都落在同一条直线上，并写出此直线的方程.
(3)设a=1,b=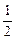
,C是以(r,r)为圆心，r为半径的圆(r＞0)，求使得点P1、P2、P3都落在圆C外时，r的取值范围.
相关试题
中，四边形
是正方形，
平面
，
是
上的一点，
是
的中点
；
，求证：
平面
.
.设方程
的系数
和
分别是先后抛掷一枚骰子得到的点数．
，当
时，其前
项和
满足
；
，求数列｛
｝的前项和
有相同的焦点，且椭圆过点
，
过点
交椭圆于
两点，且
，求直线
中，
∠
=90°，
，
⊥
.
（Ⅰ）求证：
；
的体积.推荐套卷
设数列{an}的前n项和Sn=na+n(n－1)b，(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,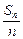－1)为坐标的点Pn(n=1,2,…)都落在同一条直线上，并写出此直线的方程.
(3)设a=1,b=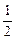,C是以(r,r)为圆心，r为半径的圆(r＞0)，求使得点P1、P2、P3都落在圆C外时，r的取值范围.
粤公网安备 44130202000953号