设f(x)是定义在R上的偶函数，其图像关于直线x=1对称，对任意x1、x2∈［0,
］,都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
(1)求f()、f(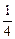
);
(2)证明f(x)是周期函数；
(3)记an=f(2n+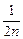
),求
中，
，
，求证：
．
，
平面
，如图．求证：直线
与平面
相交．
平面
，
，
，△
的平面角的正切值为多少．
，
为不共面直线，
，
两点在
，
两点在
，
，如图所示．求证：直线
直线
推荐套卷
设f(x)是定义在R上的偶函数，其图像关于直线x=1对称，对任意x1、x2∈［0,］,都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
(1)求f()、f();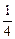
(2)证明f(x)是周期函数；
(3)记an=f(2n+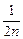),求
粤公网安备 44130202000953号